
최단 거리를 구하는 다양한 알고리즘이 있지만 오늘은 플로이드 와샬의 개념과 구현에 대해서 한번 포스팅 해보려고 한다.
1. 플로이드 와샬 알고리즘 개념
- 플로이드 와샬 알고리즘과 다른 최단 경로를 찾는 알고리즘의 차이점은 플로이드 와샬의 경우 모든 정점에서 모든 정점으로의 최단 경로를 한번에 구한다. 즉 정점과 정점, 모든 쌍의 최단 경로를 구하는 것이다.
- 방법은 먼저 가능한 모든 쌍을 표현하는 행렬(이차원 배열)을 선언하고 다이나믹 프로그래밍(dp)의 방식으로 각각의 원소들(각 쌍의 최단거리)을 업데이트 해나간다.
- 업데이트 기준를 행하는 기준은 현재 거쳐가는 정점이다
- 거쳐가는 정점을 기준으로 알고리즘을 수행한다.
- i 에서 j 로 가는데 해당 정점을 경유해서 가는 것이 더 빠르다면 그 정점을 거쳐서 가는걸로 업데이트 한다.
- 쉽게 생각한다면, j -> k 의 경로를 가는데 지날 수 있는 모든 정점(i라는 정점)을 확인하여 그 값이 최단경로라면 값을 업데이트 하는 것이다.
이해가 조금 어렵다면 플로이드 와샬을 굉장히 쉽고 간편하게 설명해주신 나동빈님 블로그에서 참고하기
먼저 플로이드 와샬을 진행하는 방법은 아래의 두가지 방법이면 끝난다.
1. Map(각 정점과의 최단거리)을 나타낼 수 있는 배열 초기화
- 문제에 나오는 형태를 참고하여 배열을 생성한다.
- 이 때, i행과 j열의 원소인 (i, j) 원소는 정점i로부터 정점j까지의 최단 경로를 뜻한다.
- 만약 각 행과 열에 해당하는 정점들이 연결되어 있다면 그 가중치로 초기화하고 인접하여 연결되어 있지 않은 정점들의 경우 INF 무한대로 초기화 한다.
- 자신과 연결되는 경우는 없기 때문에 (i, i)의 값은 0으로 초기화한다.
2. 동적 계획법(DP)의 방식으로 각 정점들간의 최단 경로를 업데이트 한다.
- 점화식의 경우 dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])의 형태를 사용한다.
- 위의 점화식을 설명한다면, i -> j로 가는 경로에서 k를 지나는 (i -> k, k -> j)의 경로가 더 작은 가중치를 가진다면 업데이트를 하겠다는 뜻이다.
- 이렇게 지나가는 모든 경로를(위의 점화식에서는 k를 의미한다.)을 차례대로 모두 검사하여 업데이트 해나간다.
아래에는 플로이드 와샬을 쉽게 이해하기 위해 나동빈님 블로그를 내 방식으로 정리해보았다.
2. 코드 구현
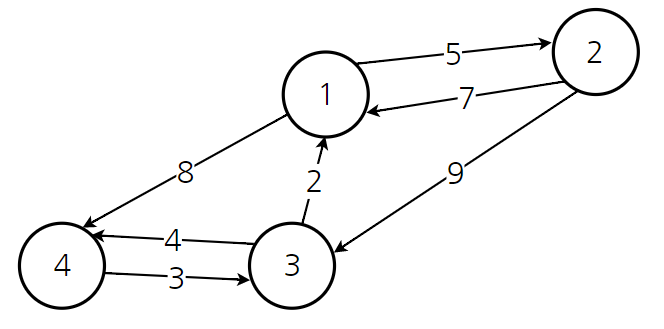
위의 그림과 같은 그래프가 문제에서 주어진다면 배열은 아래의 형태와 같을 것이다.
int a[4][4] = {
{ 0, 5, INF, 8 },
{ 7, 0, 9, INF },
{ 2, INF, 0, 4 },
{ INF, INF, 3, 0 }
};
이러한 배열을 기본으로 위의 플로이드 와샬 방법을 사용해 모든 정점들간의 최단거리를 구하면 다음과 같다.
const int INF = 2e9;
int arr[4][4] = {
{0, 5, INF, 8},
{7, 0, 9, INF},
{2, INF, 0, 4},
{INF, INF, 3, 0}
};
void solve()
{
int dp[4][4];
for(int i=0; i<4; i++)
{
for(int j=0; j<4; j++)
{
dp[i][j] = arr[i][j];
}
}
for(int k=0; k<4; k++) // k는 i -> j의 경로에서 k을 거쳐가는 경우이다
{
for(int i=0; i<4; i++) // i는 시작점 i를 나타낸다.
{
for(int j=0; j<4; j++) // j는 도착점 j이다.
{
if(i == j) // 시작지점과 도착지점이 같은 경우는 무시한다.
continue;
// 이 부분이 가장 핵심인 부분으로 i에서 j로 갈 때 k를 지나는 것이 작다면 업데이트 하는 것이다.
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]);
}
}
}
'Algorithm > 개념 구현' 카테고리의 다른 글
| 이진 탐색 / 매개 변수 탐색 (0) | 2024.08.12 |
|---|---|
| 우선순위 큐(최대힙, 최소힙), 다익스트라 알고리즘 (0) | 2024.07.29 |
| 동적 계획법 (DP) (0) | 2024.06.27 |
| MST (Minimun Spanning Tree, 최소 신장 트리) (0) | 2024.06.26 |



